Break-Even Point Definition
In accounting, economics, and business, the break-even point is the point at which cost equals revenue (indicating that there is neither profit nor loss). At this point in time, all expenses have been accounted for, so the product, investment, or business begins to generate profit.
The concept of “breaking even” has multiple applications, so the definition of break-even point varies, depending on the situation it is used.
Break-Even Point for Investments
The break-even point of an investment occurs when the market price of the investment equals its original cost. At this point, the investor has neither gained nor lost money.
If the price of the investment goes above the market price, the investment becomes profitable. However, if the price of the investment falls below the market price, the investment is not profitable.
Break-Even Point for Businesses
The break-even point for businesses occurs when revenue and expenses are equal. Alternatively, it is the amount of revenue that a business needs to earn in order to cover both its fixed and variable costs.
Before reaching its break-even point, the business will operate at a loss since its revenue doesn’t cover all of its costs. After reaching its break-even point, all costs have been accounted for, so it is able to start generating profit.
Why Is Break-Even Point Important?
The break-even point is an essential metric that can help determine whether an investment, product, or business is financially viable. It highlights the bare minimum performance required to become profitable, helping the investor or company make important decisions. Common applications include:
- Identifying the point at which the business will begin to generate profit
- Developing cost structures
- Identifying opportunities for promotions and discounts
- Establishing production goals
- Determining the optimal sales mix
- Revealing how much revenue must be earned to cover all expenses
- Determining optimal price points
- Calculating the profitability of a product or investment
- Determining how fluctuations in price or volume of sales will impact profit
- Identifying sales volume needed to hit target profit
- Establishing how far sales can decline before losses are incurred
How to Calculate Break-Even Point
The break-even point occurs when a company’s revenue is equal to its expenses, so the first step is to identify costs and selling price.
Fixed costs: costs that are independent of the number of units produced (e.g. rent, interest)
Variable costs: costs that are dependent on the number of units produced (e.g. raw materials, hourly wages)
Selling price: the price the product is sold for
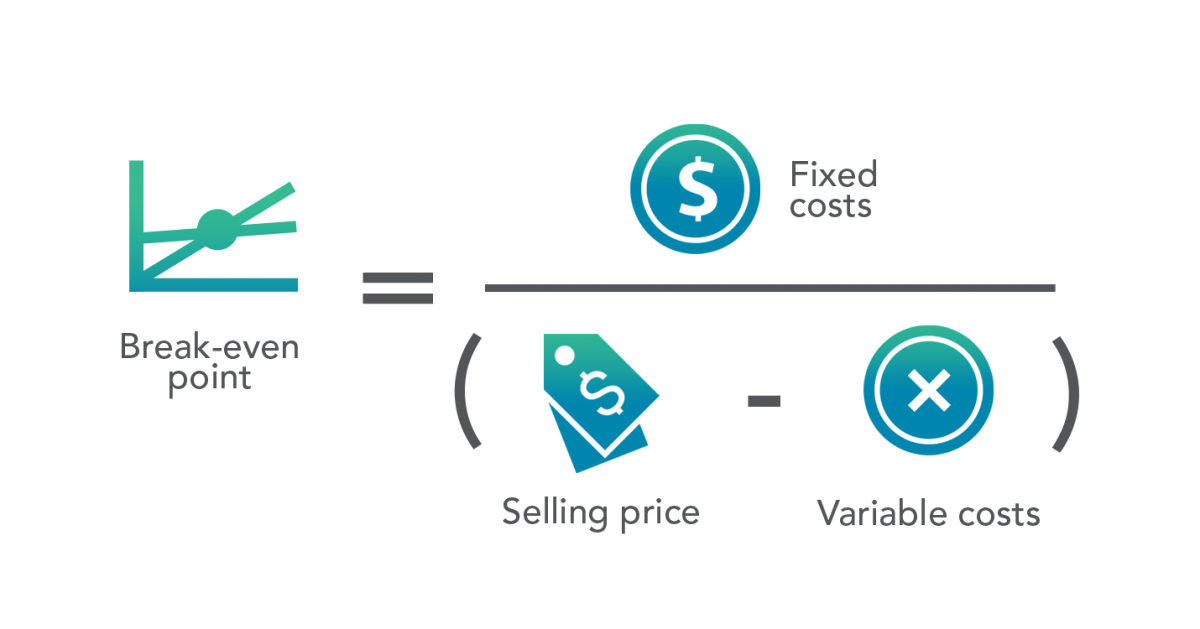
Using this data, the break-even point is calculated by dividing fixed costs by the contribution margin (selling price - the variable cost per unit). The resulting number represents the number of units the company needs to sell in order for it to break even.
Any units below this number will be sold at a loss, and any units above this number will generate profit. Until the break-even point is reached, the company’s expenses will be greater than its revenue (so it will be operating at a loss).
What Causes the Break-Even Point to Increase?
A higher break-even point means that a company must generate more revenue in order to cover its costs. There are a number of reasons why a break-even point might increase:
- Increase in fixed cost
- Increase in variable cost
- Decrease in selling price
- A change in sales mix (proportion of each product sold to total sales)
Break-Even Point Formula
You can use the following formula to calculate the break-even point:
Break-Even Point Example
Bob is considering opening a bakery that will sell a single type of bread. He is working on a business model and wants to discover whether this venture is financially viable – and when it would become profitable. Here is a breakdown of his financials:
| Fixed costs (monthly) | Variable costs (per loaf) | Selling price (per loaf) | |||
| Rent | $2,500 | Flour | $0.50 | ||
| Insurance | $250 | Water | $0.25 | ||
| Utilities | $250 | Salt | $0.10 | ||
| Advertising | $500 | Yeast | $0.15 | ||
| Total | $3,500 | Total | $1 | Total | $5 |
Using the break-even point formula above, he can calculate how many loaves the bakery will need to sell each month in order to cover all expenses:
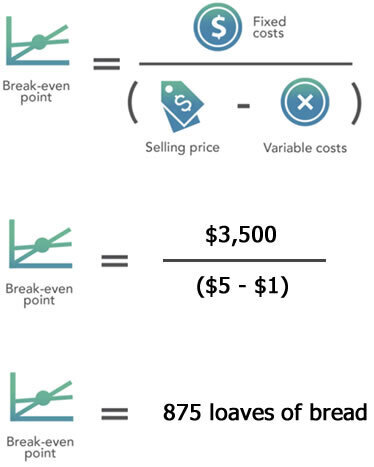
In order to break even, Bob’s bakery would need to sell 875 loaves of bread per month. If it sells fewer than 875 loaves, the business’ revenue would not cover its expenses, so Bob would lose money. However, if the bakery sells more than 875 loaves per month, it would earn enough revenue to cover all costs and generate profit.
Note: Many businesses are not profitable from the beginning because it takes time to attract customers, reduce costs, etc. Because of this, many businesses struggle to reach the break-even point before they run out of capital.
In Bob’s case, he could try to negotiate his fixed costs or find new suppliers for his variable costs, but there are no guarantees. Every situation is different and there are a number of ways to survive before a business becomes profitable.




