Options are a powerful tool that all investors need to become familiar with. Over the course of our seven-part trading course we will introduce you to the basic mechanics of not only how options work, but also how they can work for you.
Before you get started trading options, we urge you to forget the stories you may have heard about how risky they are, and how some investors have gone bankrupt using them. The truth is that options are designed to help investors limit and manage risk. Over the course of this multi-part series on options we will show you how to not only make money using options, but more important, how to save money as well.
An Introduction to Options
Investors use options for two primary reasons -- to speculate and to hedge their risk. All of us are familiar with the speculation side of investing. Every time you buy a stock you are essentially speculating on the direction the stock will move. Wall Street has coined the phrase "investing" so that buying stock does not sound so risky, but the truth is that we are always uncertain about which direction any equity investment is going to go. You might say that you are positive that IBM is heading higher as you buy the stock, and indeed more often than not you may even be right.
However, if you were absolutely positive that IBM was going to head sharply higher, then you would invest everything you had into buying the stock. All rational investors realize that there is no "sure thing" when it comes to investing, as every investment incurs at least some risk. This risk is what the investor is compensated for when he or she purchases an asset. When you purchase options as a means to speculate on future stock price movements, you are limiting your downside risk, yet your upside earnings potential is unlimited (we'll explain this in more detail later).
Aside from speculation, investors also use options for hedging purposes. A hedge is not just a little green bush in your front yard, it is a way to protect your portfolio from disaster. Hedging is like buying insurance -- you buy it as a means of protection against unforeseen events, but you hope you never have to use it. The fact that you hold insurance helps you sleep better at night. Consider this -- almost everyone buys homeowners insurance, right? But why exactly do they do this? Since the odds of having your house destroyed are relatively small, this may seem like a foolish investment to make. After all, most of us will never have a fire, flood or any other hazard that would cause us to cash in on our insurance. However, we all continue to pay our insurance premiums every year.
Why do we go on paying these hefty fees year after year instead spending the money on something we would perhaps enjoy more? The answer to this question is obv homes are very valuable to us and we would be devastated by their loss. Because of this fear of loss, most of us will happily pay someone else every year to bear this risk for us, no matter how remote the chances of loss might be. If you employ certain options strategies as a means to hedge your portfolio, you are essentially doing the same thing -- paying someone to protect you from unforeseen risks. (We'll teach you how to do exactly that over the course of this multi-part options trading series.)
Options Characteristics
Options are derivative instruments, meaning that their prices are derived from the price of another security. More specifically, options prices are derived from the price of an underlying stock. This will all become very clear shortly.
Another important thing to understand is that every option represents a contract between a buyer and seller. The seller (writer) has the obligation to either buy or sell stock (depending on what type of option he or she sold -- either a call option or a put option) to the buyer at a specified price by a specified date. Meanwhile, the buyer of an options contract has the right, but not the obligation, to complete the transaction by a specified date. When an option expires, if it is not in the buyer's best interest to exercise the option, then he or she is not obligated to do anything. The buyer has purchased the option to carry out a certain transaction in the future -- hence the name.
Here are a few terms you must first become familiar with before trading options:
Option Buyer (Option Holder) -- Party that purchases and holds the options contract.
Option Seller -- Party that writes, or creates, the options contract.
Strike Price -- The price at which the option seller agrees to buy or sell a certain stock in the future.
Expiration Month -- The month in which the option will expire.
Expiration Date -- This is always the third Friday of the month in which the option is scheduled to expire.
Option Contract -- Each options contract represents an interest in 100 shares of a certain underlying stock.
put option -- This type of option gives the option holder the right, but not the obligation, to sell 100 shares of a particular underlying stock at a specified price (the strike price) on a specified date (the expiration date). For example, let's say you were to purchase a put option on shares of Microsoft (MSFT) with a strike price of $50 and an expiration date of March 19th. This option would give you the right to sell 100 shares of Microsoft at a price of $50 on March 19th (the right to do this, of course, will only be valuable if Microsoft is trading below $50 per share at that point in time).
Call Option -- This type of option gives the option holder the right, but not the obligation, to purchase 100 shares of a particular underlying stock at a specified strike price on the option's expiration date. For example, let's say you were to purchase a call option on shares of Intel (INTC) with a strike price of $40 and an expiration date of April 16th. This option would give you the right to purchase 100 shares of Intel at a price of $40 on April 16th (the right to do this, of course, will only be valuable if Intel is trading above $40 per share at that point in time).
"In-The-Money" Option -- An option that, if it were exercised today, would be worth more than $0. In the case of a call option, the option is only considered to be "in-the-money" when the price of the underlying stock is greater than the option's strike price. So, in the case of our Intel example above, the call option will be "in-the-money" when shares of Intel are trading above $40. Meanwhile, in the case of a put option, the option is only considered to be "in-the-money" when the price of the underlying stock is less than the option's strike price. So, in the case of our Microsoft example, the put option will be "in-the-money" only when shares of Microsoft are trading below $50 per share.
"Out-Of-The-Money" Option -- An option that, if it were exercised today, would not be worth a single cent. In the case of a call option, the option is considered to be "out-of-the-money" when the price of the underlying stock is less than the option's strike price. So, in the case of our Intel example above, the call option will be " out-of-the-money " when Intel is trading below $40 per share. After all, if Intel is trading for less than $40 (let's say it is at $35), then the right to purchase Intel at a price of $40 per share is completely worthless (if you can buy the stock in the open market for $35, then you certainly wouldn't want to buy it for $40). Options traders use the term "out-of-the-money" to describe this type of situation. The analysis is similar when it comes to put options. In the case of a put option, the option is considered to be "out-of-the-money" when the price of the underlying stock is greater than the option's strike price. So, in the case of our Microsoft example, the put option will be "out-of-the-money" when shares of Microsoft are trading above $50 per share.
"At-The-Money" Option -- An option is considered to be "at-the-money" when its strike price is exactly equivalent to the price of the underlying stock.
Example: Call Option Contract
As a quick example, let's say IBM stock is currently trading at $100 per share. Now let's say an investor purchases one call option contract on IBM at a price of $2.00 per contract. Note: Because each options contract represents an interest in 100 underlying shares of stock, the actual cost of this option will be $200 (100 shares x $2.00 = $200).
Here's what will happen to the value of this call option under a variety of different scenarios:
When the option expires IBM is trading at $105.
Remember: The call option gives the buyer the right to purchase shares of IBM at $100 per share. In this scenario, the buyer could use the option to purchase those shares at $100, then immediately sell those same shares in the open market for $105. Because of this, the option will sell for $5.00 on the expiration date (since each option represents an interest in 100 underlying shares, this will amount to a total sale price of $500). Since the investor purchased this option for $200, the net profit to the buyer from this trade will be $300.When the option expires IBM is trading at $101.
Using the same analysis as shown above, the call option will now be worth $1 (or $100 total). Since the investor spent $200 to purchase the option in the first place, he or she will show a net loss on this trade of $1.00 (or $100 total).When the option expires IBM is trading at or below $100.
If IBM ends up at or below $100 on the option's expiration date, then contract will expire out-of-the-money. It will now be worthless, so the option buyer will lose 100% of his or her money (in this case, the full $200 that he or she spent for the option).
Selling Options
Selling options is another aspect of trading that investors should become familiar with. Up to this point we have only discussed the purchase side of options. Sometimes, however, it is in the investor’s best interest to sell, or write, options. When you write options, you'll have a very different set of risks/rewards versus purchasing them. But before we delve into that topic, let's first take a look at the two forms of options writing:
· Covered -- The writer of the option owns the underlying stock or asset.
· Naked -- The writer of the option does not own the underlying stock. In this instance the writer is most likely speculating on the direction the stock will move and not hedging a position.
The safest way to sell an option is to write what is known as a "covered call". This strategy is so safe, in fact, that it is suitable for most retirement (IRA) accounts. In this type of trade, the investor sells a call option on an underlying stock that he/she already owns. This trade is usually made in an effort to generate additional income from a particular holding.
Here is how the process works:
Assume that in January an investor owns 100 shares of IBM stock, which currently trades at $100. Over the course of the next month, the investor does not believe that IBM will trade for more than $105. With this expectation, the investor would be wise to sell an option contract on IBM for $105 to another investor who feels differently. Suppose that an IBM FEB 105 option sells for $3. The investor who writes the option will therefore receive $3 today (or $300 total, since each option represents an interest in 100 underlying shares) in exchange for selling the option (even though the option does not expire until next month).
Now consider the following scenarios:
IBM trades at $110 at expiration. In this scenario, the writer was too conservative in his estimate of where IBM would trade this month. The writer will therefore be obligated to sell 100 shares to the buyer of the call option for $105 each. The net impact to the options seller is $105 (for selling the stock) + $3 (for selling the option) to yield $108. This will be the net result for the seller no matter how high IBM's shares soar. So, as you can see, by selling a covered call, the option writer has limited his/her upside potential. In return, he/she received $300 for the sale of the option contract.
IBM trades at $103 at expiration. In this scenario, the writer was accurate in his/her estimate. The writer is not obligated to sell his/her shares because the buyer would not want to buy them at $105 (after all, the buyer could instead purchase them in the open market for just $103). The net result is that the investor generates $300 in additional income while still keeping his/her stock, which also gained $300 during the month.
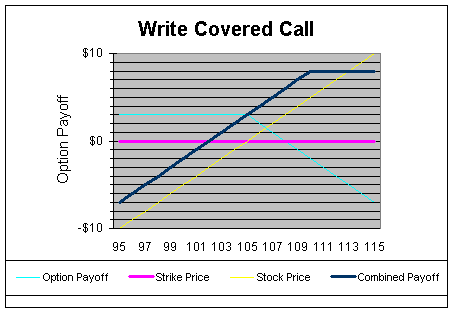
The covered call strategy works best when the investor plans on holding the underlying stock for a long period but does not expect a significant increase in the near term. As you can see from the diagram above, the investor is limiting his/her upside potential to $8 in return for a guaranteed $3 premium. If shares of IBM tank, then the investor's losses can still be significant. However, if the stock declines, then thanks to the options sale the investor will always be $3 better off than if he/she had merely held the stock alone. (Please note that you can also employ a similar strategy by shorting a stock and selling a put against the position. This is referred to as writing a covered put.)
Naked Option Writing
When an investor writes an option on a stock he/she does not own, it is referred to as writing a “naked” options contract. This strategy is mainly used for speculating. The investor must be very confident about the direction the stock will go and have the resources available to cover any mistakes.
For obvious reasons, naked option writing is only available to experienced or expert traders. This is because the investor is taking on a possibly unlimited amount of risk in exchange for a fixed premium. Why is the potential risk unlimited when it comes to selling naked options? Well, in the example above, the investor already owned IBM stock, so even if IBM rapidly appreciated (the worst-case scenario), the investor could simply sell his/her stock for a lower-than-market price. However, if the investor had written a naked call option (in other words, he/she did not own IBM and still sold this call option), then the result could have been devastating.
Suppose that IBM developed a revolutionary technology and the stock price doubled in a short period of time to $200 (not a likely scenario, but it can happen nonetheless). The investor who sold the option for $3 would now have to sell IBM stock to the option purchaser for the agreed upon price of $105. However, the market price of IBM stock is now $200. In order to deliver the stock to the option buyer, the option writer must purchase IBM in the open market for $200, then sell those same shares immediately to the option buyer for $105. If you factor in the $3 that the option writer initially received for selling the contract, then his/her total losses would be a whopping $92 per contract in this case.
Note: To offset this risk of dramatic losses, some investors will sell an option with a lower strike price and simultaneously purchase an option with a higher strike price. This technique lowers the return the investor receives, but it also limits the losses that he/she might incur.
Conclusion
There are many instances in which you might find selling options appropriate. If you are determined to hold on to a particular stock for the long haul, then we suggest look into the process of writing covered calls. This technique will help you add real income to your portfolio and compliment your holdings. If you plan to hold a stock for the long haul anyway, then the worst that can happen is you might be forced to sell your stock at the end of the month (but for a price you would gladly have accepted at the beginning of the month). You should note that in the long run, since options tend to lose their value as they approach their expiration date, options sales tend to be much more profitable than options purchases. If you decide to sell options naked, then please use extreme caution and be cognizant of losses you might face. This strategy may work 9 out of 10 times, but you better be prepared for the one time it may dramatically go against you.
Portfolio Hedging
Many times it is in an investor’s best interest to lock in recent gains or to protect a portfolio of stocks from a decline beyond a certain price. One way to do this would be to purchase a put option contract on each of your various holdings (this would essentially allow you to "lock in" a particular sale price on each stock, so even if the market crashed, your overall portfolio wouldn't suffer much). However, if you hold a large, diversified portfolio of stocks, then it is probably not cost-effective to insure each and every position in this manner.
As an alternative, you might want to consider using index options to hedge the risk in your portfolio. Index options are options not on an individual stock, but rather on an entire index. Many different indices have options available, including the Nasdaq 100, the Dow Jones Industrial Average and the S&P 500. For the purposes of today's example we will use the S&P 500-- ticker symbol "SPX"--as a proxy for the overall market's return. With some careful planning, you should be able to offset a sharp decline in your portfolio by hedging your overall position with index options. Though it is impossible to forecast exactly how your portfolio will perform during a steep market sell-off, you can calculate this out fairly close to the actual result.
Before you can hedge your portfolio against a major market correction, however, you'll need to figure out two key items. First, you'll need to determine which particular index to use as a proxy for your portfolio. If you hold primarily high-tech stocks (or if you just want to hedge against a downfall in your technology holdings), then you might want to consider trading options on the Nasdaq 100. Alternatively, if your portfolio consists mainly of blue-chip companies, then you might want to use the Dow Jones Industrial Average. Again, since we're going to assume that your portfolio consists of a well-diversified mix of different stocks, for the purposes of today's example we'll use the S&P 500 as our proxy.
Next, you'll need to find the correct number of options to use as a portfolio hedge. Along those lines, here are a few important items to consider:
-- You first need to derive an estimate of beta (?). This may sound like an obscure technical term, but beta simply measures the amount of variance in a portfolio in relation to the market. If you were using the S&P 500 as a proxy for the market, then ? would indicate how much your portfolio moves when the S&P 500 changes by 1%. For example, if you notice that, in general, your portfolio changes by 2% whenever the S&P moves up 1%, then your portfolio has a ? of 2.0. If the portfolio changes by 0.5%, then ? = 0.5. If the portfolio changes by 1%, then ? = 1.0. (Beta is an important component of all options, so it would be a useful exercise to try this with your portfolio or individual stocks to become more comfortable with this term.)
-- The next step is finding the risk-free rate. As the name implies, this is the rate of interest that can be obtained without incurring any risk. For the short-term, we usually use the appropriate three-month T-bill rate.
-- If your portfolio pays any dividends, then you need to formulate the portfolio’s dividend yield. This can be found by adding the amount of dividends paid during the year and dividing that figure by the value of your portfolio. For example, if you receive roughly $40,000 in dividends per year on a $1 million portfolio, then your portfolio's dividend yield is 4% (40,000 ÷ 1,000,000).
Now consider the following example:
Suppose you own a $1 million portfolio of stocks and you wish to insure this portfolio against a decline of greater than -6% during the next three months. In other words, you want to put a hedge in place to make certain that your portfolio does not fall below $940,000. To make the calculations fairly simple, let's assume that the S&P 500 index is currently trading at 1000. Let's also assume that your portfolio is volatile and generally doubles the S&P 500’s gains or losses. Therefore, the ? is 2.0. Finally, let's assume that the risk-free rate is 4% and the dividend yields on both your portfolio and the S&P 500 are also 4%. The assumed return of the SPX is 12% per year. (We should note that it is not necessary to have an accurate forecast of the market's return for this hedge to work correctly.) In this example, if you want to employ SPX put options as a hedging tool, then here's how to calculate how many contracts you need to purchase:
Total Return of SPX in Three Months:
In three month’s time you expect a 3% return (assuming a 12% annual rate) and a 1% dividend (assuming a 4% annual yield) for a total return of 4%.
Excess Return of SPX:
The excess return of any asset is the amount it returns over the risk-free rate. In this case, the risk-free rate would be 1% (assuming a 4% annual rate) in three months. The excess return is therefore 3% (4% total return – 1% risk-free).
Total Return of Portfolio in Three months:
For this example we stated that the ? of the portfolio is 2, which implies that if the market returns 3%, then your portfolio will double that amount by returning 6%. The expected dividend is still 1% during the next three months, so the total expected return will be 7%.
Excess Return of Portfolio:
The expected excess return is 7% and the risk-free rate is 1%, so the excess return here will be 6%. This is the return you expect in three month’s time.
The table below illustrates how the portfolio is expected to behave in relation to the market:
| Value of S&P 500 Index in Three Months | Value of Portfolio in Three Months |
| 1060 | $1,120,000 |
| 1030 | 1,060,000 |
| 1000 | 1,000,000 |
| 970 | 940,000 |
| 940 | 880,000 |
From this chart we can see that the portfolio will perform twice as well, or twice as poorly, as the market. In this example, you do not want to let your portfolio fall below $940,000 in the next three months. Using the table, you can see that buying SPX puts with a strike price of 970 will accomplish this. To find the optimal number of put option contracts to purchase, use this formula:
Portfolio Value ÷ [(100 x Current Strike Price) ÷ ?] = number of put contracts
In this example, where the portfolio value equals $1,000,000 and the current strike price is 1000, the calculation would be as follows:
$1,000,000 ÷ [(100,000) ÷ 2] =
$1,000,000 ÷ 50,000 = 20 put contracts
This means you should buy 20 SPX 970 Put contracts that expire in three months to insure your portfolio against a decline below $940,000.
To see that this is correct, suppose the SPX finishes at 940 when the options expire in three months. This implies from the chart that your portfolio would be worth just $880,000. However, the SPX 970 Put contract will expire "in the money" and will be worth $30 (970 – 940) at expiration. In this scenario, your 20 options contracts (each contract is for 100 options) will now carry a value of $60,000. When you add that figure to the $880,000 that your portfolio is now worth, this equals exactly $940,000. You can perform this procedure for any decline in the SPX, and in every case you will find that your overall portfolio will still be worth a minimum of $940,000 at expiration.
Conclusion
Portfolio hedging is an important technique to learn. Although the calculation of ? must be correct to ensure an exact result, most investors find that even a reasonable approximation will deliver a satisfactory hedge. This technique is especially helpful when an investor has experienced an extended period of gains and feels this increase might not be sustainable in the future. Like all option strategies, portfolio hedging requires a little planning before executing a trade. However, the security that this strategy provides could make it well worth the time and effort in a period of declining stock prices.
The Five Basic Components of Options Pricing
After you have decided whether you are hedging or speculating with your options purchase, you will then need to determine which specific options fit your needs.
When looking up an options quote -- more commonly referred to as an options chain -- you will notice that there are a barrage of choices available to you. Simply knowing that you wish to hedge or speculate is not sufficient. You will need to determine if your desired strategy requires you to trade a put or a call option, how long you wish the expiration date to be, and what strike price you would like to trade. Before trading options, it is important to familiarize yourself with the factors that impact options prices so you choose the best one to meet your needs.
Factors that determine option pricing:
Option pricing is determined using a complex differential equation formulated by Myron Scholes and Fischer Black in 1973. In 1997 these two professors were awarded the Nobel Prize for their efforts. The Black-Scholes formula in detail and its explanation are beyond the scope of this article. Fortunately, however, it is not necessary to understand the model’s intricacies in order to make proper option trades.
The five basic components of option pricing include the following:
Underlying Asset Price -- The price of the underlying stock or index the option is written on.
Asset Volatility -- Amount of uncertainty associated with the asset’s expected return. In general, the higher the volatility the more expensive the option will be. For example, if an asset’s value is $100 today, and next month the price is estimated to be either $125 or $75, then the amount of uncertainty here is very high. Because of this, the option price will be high as well (after all, the more volatile the security, the greater chance that it will deliver large returns for the option holder). This uncertainty of return is one of the main drivers of option prices.
Time to Expiration -- The amount of time left before the option expires. The price of an option decreases as it approaches its expiration date. Why is this the case? Well, as the expiration date approaches, the chances of the option gaining in value become lower and lower because the underlying security has less time in which to make a major up or down move.
Risk-free rate -- For a variety of reasons that are beyond the scope of this article, the rate of return that may be earned without bearing any risk also comes into play when pricing options. Normally this is assumed to be the rate of interest earned by U.S. Treasury bills.
Option Strike Price -- This is the price at which the option can be exercised.
All of these factors play an important role in determining every option’s price. The only two factors that an investor has any control over, however, are time to expiration and the strike price (this is assuming, of course, that you've already chosen the security on which you're going to trade the option). Because of this, investors should concentrate their efforts on choosing the appropriate strike and expiration that best suits their needs. The following are rules of thumb for what hedgers and speculators should consider:
Hedging:
Use Puts -- Investors are generally long the market. In other words, they generally own stocks but do not short them. To offset the risk of owning a large stock portfolio (or large individual stock position), you can buy put options that will increase as your portfolio (or individual stock) declines. By purchasing put options, investors can limit the amount of money they will lose if the market plummets.
Longer Expiration -- Investors normally hold stocks for longer periods than speculators and therefore buy insurance for longer periods of time. They tend to purchase options with longer expiration dates.
Out-of-the-Money Options -- Most investors are concerned with buying insurance to protect their capital from falling below a certain amount. This amount is generally somewhere below where the current stock price is.
Speculating:
Use Calls -- Speculators usually purchase options on a particular stock rather than the actual stock itself. Why? Well, if the speculator is correct in predicting the direction of the stock, then he or she will make far more money by holding options thanks to the leverage that options provide. An investor can control a large amount of stock with a very small amount of money by utilizing options.
Short Expiration -- Speculators usually expect a move in a stock in a short amount of time. Therefore, they often buy less expensive options with short expiration dates.
In-the-Money Options -- Many different trading strategies existing, but in general, speculators often buy in-the-money options so they can capture profits more quickly from rising stock prices.
There are a number of risk/reward characteristics of in- or out-of-the-money (ITM/OTM) options that all investors should consider. An ITM option will cost significantly more money to purchase, but the probability that it will at least have some value at expiration will be far greater. An OTM option will cost less money up front, but the probability of it expiring worthless will be much higher. The reason investors purchase OTM options is due to the fact that a correct bet can lead to very significant gains of many times your purchase price. Meanwhile, the potential downside from such a purchase is usually a total loss.
Sometimes it can help to visualize what happens when a trade is made. The diagram below illustrates an example of what a sample option will be worth, as well as the gain/loss to the investor who made it. Once again, we will use shares of IBM as an example.
Let's suppose it is January and the stock is currently trading at exactly $100 per share. An investor who owned 100 shares of IBM and wanted to hedge against a loss until the 3rd Friday in February would likely purchase a February 100 put option contract on IBM. This means that the buyer of the put would essentially be insured against a loss below $100, less the cost of the option. In this example, we will assume the option cost is $3. This means that no matter what happens, the investor’s position in IBM will not be worth less than $97 ($100 - $3 option cost) by expiration in February.
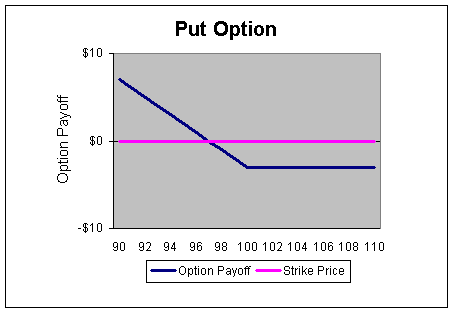
In this example, we can see that the put option increases in value as the stock price declines below $100. If IBM is trading above $100 per share on the third Friday in February (the expiration date in this example), then the option will expire worthless and the investor will lose his or her entire option premium. But since the investor in this example actually owns IBM shares, this will likely be of little consequence.
However, if IBM tumbles to $90 at expiration, then the investor will have lost $10 on the stock. Thankfully though, this investor decided to hedge his/her position by purchasing a put option. And since put options rise in price as the underlying security falls, this particular option will have soared in value.
It will now be worth $10. Subtract the cost of the option, $3, and we can see that the investor's net position will be worth exactly $97. It's important to note that the value of the investor's position will remain $97 even if the price of IBM drops to zero! So, as you can see, purchasing put options against stocks that you own in your portfolio will require you to pay option premiums, but it will also protect you from suffering catastrophic losses if the market nosedives.
This strategy is especially useful if you're looking to lock in gains after a stock has experienced a significant run-up. You may still believe the stock will appreciate more, but you might also be unwilling to let it decline below a certain point.
Sticking to our same example above, consider what would happen if IBM had just skyrocketed to $100 in a brief amount of time (before the investor purchases the put option). In this case, the investor might be tempted to exit the position to lock in his/her gains. Although the investor could sell the stock immediately at $100, he/she could also use the option strategy above (purchasing a FEB 100 put option) to limit any potential future losses to just $97. If the stock were to subsequently appreciate to $120, then the investor who sold his/her shares would not participate in the additional $20 gain.
However, if the investor utilized the put option purchase, then he/she would have enjoyed the safety of locking in a minimum stock price (in this case $97), while still being able to participate in further gains. So, if IBM soared further, jumping from $100 to $120, then the investor's net position would still be worth $117 ($120 for the stock minus $3 to purchase the option). That's a small sacrifice to make for securing a gain!
Spread & Combination Trades
A virtually limitless number of options trading strategies are available to investors. In this installment of our series on options trading, I will discuss two more advanced strategies -- the spread trade and the combination trade. Both of these trades involve taking two option positions on the same stock.
Spread Trades
In a previous options lesson we discussed the process of writing a covered call. As you may remember, this involves selling an option on a stock that you currently hold in your portfolio. A spread is very similar to a covered call, except it basically involves covering an option instead of the underlying stock. An investor should utilize this particular strategy if he/she feels that a stock will move in one direction but believes the gains will be limited.
To execute a spread trade, the investor must buy an option at one strike price, then sell an option at a strike price that is farther out-of-the-money (both contracts should expire in the same month). Since this type of trade involves the sale of an option, the trader will receive initial income from this transaction. The income received will not be enough to offset the cost of buying the first option, but it will lower the overall cost of the trade. However, in exchange for this lower transaction cost, the investor will essentially forfeit any gains that he/she would have earned above a certain set level.
To gain a better understanding of how a spread trade works, let's take a look at an example...
Let's suppose shares of IBM are trading at $100 and the trader in our example has no current position in the stock. By the time of option expiration the trader feels that IBM will likely trade above $105, but will not climb higher than $110. Let's assume that the price of an IBM 105 call option is $3. Meanwhile, the IBM 110 calls are selling for $1. To maximize the profit potential from this type of scenario, the investor would probably decide to purchase a spread. To do this, he or she would buy the IBM 105 call for $3 and at the same time sell the IBM 110 call for $1. The net result of these two transactions would be a debit to the trader of $2 ($3 paid to purchase one option - $1 received for the sale of the other option).
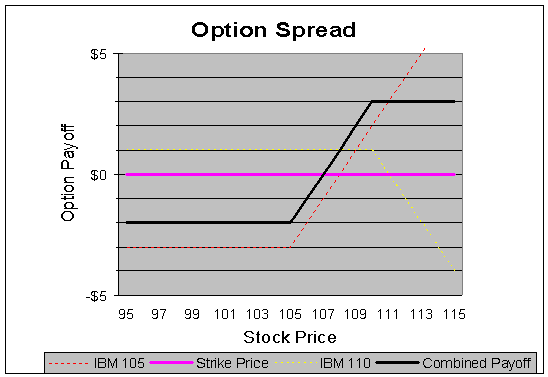
There are a variety of different ways to use spreads when trading. Another commonly used spread is called a calendar spread. In this type of spread, an investor believes that a particular stock will move to a certain price, but will not do so during the current period of time. With this in mind, to execute a calendar spread the investor would buy an option (usually out-of-the-money) with an expiration date later in the year and would simultaneously sell an option that is set to expire closer to the present time. The desired result is for the option sold with the closer expiration date to expire worthless, yet for the stock to come close to its strike price. The investor would then keep the option premium earned on this sale and would use the proceeds to offset the cost of purchasing the other option.
Combination Trades
A combination is an option strategy where the trader takes a position in both call and put options in the same underlying stock. For the sake of example, in this section we will look at a very popular trade called a long straddle. In this particular type of trade, an investor will purchase both a call and put on the same stock, and both of these options will have identical strike prices and expiration dates.
It may initially sound counterintuitive to be on both the long and short side of the same stock. After all, if you're only trading regular common stocks, it doesn't make sense to be both long and short at the same time. In the wonderful world of options, however, it is sometimes beneficial to enter into this type of trade. Straddles are designed to allow investors to profit from a large move in a given stock. The beautiful thing about them is that the actual direction the stock takes does not matter, the only thing that matters is whether the stock makes a substantial move. This is the key point to trading straddles. An investor does not have to be certain which direction the stock will move; just certain it will move strongly one way or the other. Because of this, straddles make an excellent choice in choppy markets where the only certainty is high volatility.
Let’s take a look at an example of how a straddle trade works...
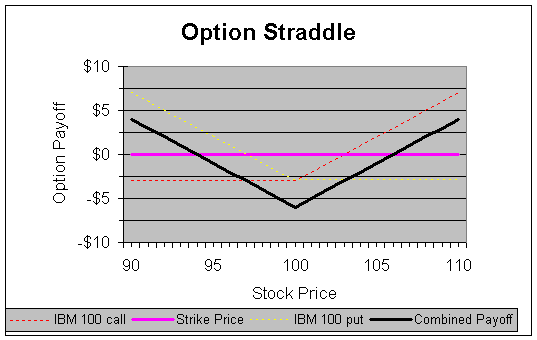
As you can clearly see in the payoff diagram of this trade above, this particular straddle will be profitable if the price of the stock moves more than $6 in either direction by the time the options expire. If the price remains at exactly $100, then the investor will suffer a maximum loss of $6. Once the price of IBM's underlying shares moves beyond $94 or $106 the investor will begin to realize a profit from the trade. If the price does indeed move at least 10%, as the investor predicted, to either $90 or $110, then the profit will be $4 ($10 sale of option - $3 purchase of call - $3 purchase of put).
Both spreads and straddles are designed to limit an investor’s losses yet still allow him/her to realize significant gains. By using multiple option positions at the same time, you can create powerful tools to help you earn greater returns as well as manage risk in your portfolio. With some planning and a little practice you can use the same techniques that professional traders employ to earn above-average profits.
Collar & Butterfly Trades
There are two final strategies that options investors should be aware of: collars and butterflies. Although these two are not as widely used as the other strategies we've detailed previously, they can often prove very useful when the situation is right.
Collar
A collar is an interesting strategy that is often employed by major investment banks and corporate executives. This position is made by selling a call option at one strike price and using the proceeds to purchase a put option at a lower price. The cost to the investor to make this trade, therefore, is essentially zero.
Investors who hold a large position in an underlying stock and wish to liquidate their holdings at some time in the future commonly use this type of trade. Why? Well, the collar allows them to lock in a particular sale price (in actuality, it ends up being a range between two prices) ahead of time. In other words, after implementing the collar trade, they then know the exact highest and lowest dollar amounts they could potentially receive when they sell their underlying stock. Speculators do not commonly make this type of trade since it is a high-risk, low-reward scenario unless you hold the underlying stock. However, if the investor already owns the underlying stock, then the trade is very low-risk and low-cost.
Example:
Judy is an executive at IBM and has recently been awarded a significant amount of IBM stock, which is currently trading at $100. She feels strongly about IBM’s prospects over the next three months, but she remembers that many other people who worked at high-tech firms had the same belief in the 1990s when the Internet bubble collapsed. Most of these people lost virtually all of their investment. In this particular case, however, Judy cannot afford to lose her entire investment. On the other hand, she would also like to try to get $10 more for per share her stock, or $110.
After assessing her personal financial situation, Judy determines that she cannot afford to sell her shares for anything less than $90. To hedge her current holdings, she decides to institute a collar trade. (This trade gets its name because the position is essentially "collared" between two prices.) It is currently January, and to collar this position for three months she sells one IBM MAR 120 call for every 100 shares she owns. With the amount she receives from this sale she simultaneously buys one IBM MAR 80 put for every 100 shares that she owns (we will assume that both sides cost $5 each). Since both of these options cost the same price, the net cost of this initial trade was $0 to her. With this trade, Judy now knows that no matter what happens, she will receive an amount between $90 and $110 if she decides to sell her IBM shares when the options expire in March.
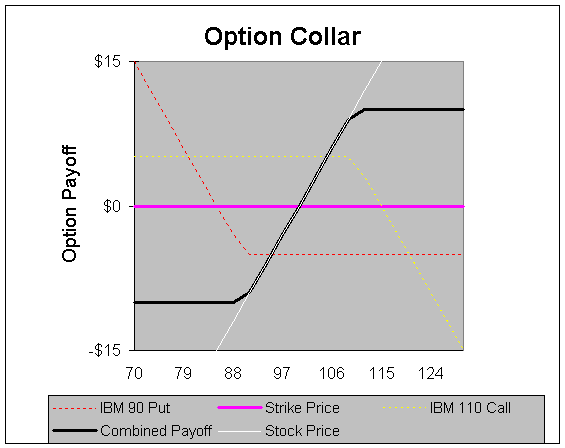
As the graph above illustrates, Judy's total profit or loss from the combinations of these positions is limited to $10. This means that if IBM rockets up to $200, the most Judy will receive is $110. Conversely, if IBM crashes to $20, the least she will receive is $90. For an investor who is comfortable with either of the two scenarios, this is an excellent hedging strategy.
Butterfly
Traders often use the butterfly strategy when they feel a particular stock will remain neutral during a certain period. By entering into a butterfly trade, the trader is essentially betting that the underlying stock price will remain close to where it is currently. This trade requires three separate positions (four total contracts), and is therefore a bit more complex than the collar. It can be made using either put options or call options. For simplicity, we will use calls in this example. To execute this trade, the investor will need to buy two calls -- one at a low strike price and one at a higher strike price. The investor also needs to sell two options with strike prices at or near the current price. In the end, this type of trade will pay the maximum amount if the stock finishes at the middle strike price. The trade has very limited downside risk, but the trader must estimate the correct future stock price to a fairly narrow range in order to make the trade profitable.
Example:
An investor believes that IBM, which is once again trading at $100, will remain relatively unchanged during the next month. To take advantage of this, but also desiring to limit downside risk, the trader sets up a butterfly trade. To do this, the trader buys one IBM 95 call for $6 and one IBM 105 call for $1. The trader will also sell two IBM 100 calls for $3 each. The net result of all of these positions will be a cost of just $1 to the trader, as shown below:
Option Trade | Cost |
Sell 2 IBM 100 calls | +$6 |
Buy 1 IBM 95 call | -$6 |
Buy 1 IBM 105 call | -$1 |
Total | -$1 |
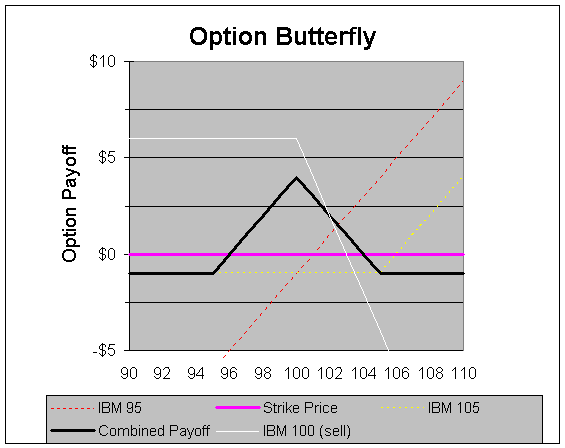
A butterfly trade may seem complicated at first glance due to the large number of options positions required to construct it. However, a quick look at the diagram above should make the payoff relatively easy to understand. In this example, the trader obtains the maximum payoff when the stock finishes at $100. As IBM's price moves further and further from $100 in either direction, the trade begins to lose value. When the price reaches (or moves beyond) $95 or $105, the trade then leads to a maximum loss of $1. This diagram clearly shows just how accurate the trader must be at forecasting IBM's future stock price in order to reap a profit from the trade. If the outcome does not go according to plan, however, then the worst that can happen is the trader loses $1, no matter how high or low the price goes.
Conclusion
The two options strategies outlined above -- the collar and the butterfly -- should only be used in very specific situations. However, when used effectively, they can be extremely profitable. A collar can help lower your volatility during an uncertain time period and can help you lock in a range of sale prices for a stock you currently own. Meanwhile, the butterfly is a good strategy for periods where a stock is not likely to fluctuate to a great degree. The butterfly trade can change what would normally be an unprofitable trading period for the stock into a profitable one.
Intrinsic Value vs. Time Value
In this installment of our options series we'll cover two very important topics--intrinsic and time value. These two concepts are what comprise an option’s price. By being familiar with these terms and knowing how to use them, you'll find yourself in a much better position to choose the option contract that best suits your particular investment needs.
Intrinsic Value -- This is the value that any given option would have if it were exercised today. It is defined as the difference between the option's strike price (X) and the stock's actual current price (CP). In the case of a call option, you can calculate this intrinsic value by taking CP - X. If the result is greater than zero (in other words, if the stock's current price is greater than the option's strike price), then the amount left over after subtracting CP - X is the option's intrinsic value. If the strike price is greater than the current stock price, then the intrinsic value of the option is zero--it would not be worth anything if it were to be exercised today (please note that an option's intrinsic value can never be below zero). To determine the intrinsic value of a put option, simply rintrinsic valueerse the calculation to X – CP.
To illustrate, let's say IBM stock is priced at $105. In this case, an IBM 100 call option would have an intrinsic value of $5 ($105 - $100 = $5). However, an IBM 100 put option would have an intrinsic value of zero ($100 - $105 = -$5 ---> since this figure is less than zero, the intrinsic value is zero. Again, intrinsic value can never be negative.). On the other hand, if we were to look at an IBM put option with a strike price of 120, then this particular option would have an intrinsic of $15 ($120 - $105 = $15).
Time Value -- This is the second component of an option’s price. It is defined as any value of an option other than its intrinsic value. Looking at the example above, if IBM is trading at $105 and the IBM 100 call option is trading at $7, then we would say that this option has $2 of time value ($7 option price - $5 intrinsic value = $2 time value). Options that have zero intrinsic value are comprised entirely of time value. Time value is basically the risk premium that the seller requires to provide the option buyer with the right to buy/sell the stock up to the expiration date. Think of this component as the “insurance premium” of the option.
Time value is easy to see when looking at the price of an option, but the actual derivation of time value is based on a fairly complex equation. Basically, an option's time value is largely determined by the amount of volatility that the market believes the stock will exhibit before expiration. If the market does not expect the stock to move much, then the option's time value will be relatively low. Meanwhile, the opposite is true for stocks that are expected to be very volatile. For example, if IBM stock is priced at $100 and the IBM 100 call is priced at $5, then the market is expecting at least a 5% ($5 / $100) upside move prior to expiration. High-beta stocks, or those that tend to be more volatile than the general market, usually have very high time values because of the uncertainty of the stock price prior to an option's expiration.
Conceptually, this all makes perfect sense. After all, if you are an options seller, then you will probably be willing to sell options at very low prices on shares of, let's say, a slow-moving utility stock like Southern Company (SO). On the other hand, if you were to sell options on shares of a highly volatile stock like Amazon.com (AMZN), then you would require much greater compensation. After all, Amazon's stock has a much greater chance of moving quickly in one direction or the other, which could end up costing you a great deal of money if the stock moves in a favorable direction for the option buyer.
Another important thing to understand about time value is that it decreases as an option gets closer and closer to expiration. Why is this the case? Well, the easiest way to think about this is that as the option approaches expiration, the underlying stock has less and less time to move in a favorable direction for the option buyer. For example, assuming that both options were trading at the same price, would you rather purchase an IBM 110 call option that expires this month or one that expires next year? From a buyer's perspective, you would obviously rather purchase the one that expires next year. After all, the chances of IBM moving above $110 within the next year are likely to be far greater than the chances of it soaring that high within the next month.
In the real world, of course, these two call options would not likely trade at the same price. Because the option that expires next year has a better chance of moving higher, its time value will be significantly greater. In this regard, options are priced somewhat like insurance; the longer the time horizon, the more expensive they will be.
One other key item to note is that the further "in-the-money" (please see lesson #2 if you are unfamiliar with this term) an option is, the less time value it will have. Options that are deep "in-the-money" generally trade at or near their actual intrinsic value. This is because options with a significant amount of intrinsic value built in have a very low chance of expiring worthless. Therefore, the primary value they provide is already priced into the option in the form of their intrinsic value.
When using options in future, we hope you will consider each option's intrinsic and time values to help you determine which contracts to choose. In general, remember that options that are further "in-the-money" are less likely to expire worthless and therefore have less risk of loss. On the other hand, they are much more expensive to purchase. Options that are out-of-the-money have a high risk of expiring worthless, but they tend to be relatively inexpensive. As the time value approaches zero at expiration, "out-of-the-money" options have a greater potential for total loss if the underlying stock moves in an adverse direction.



