What Is CAGR?
CAGR stands for compound annual growth rate. A widely-used measure of growth, CAGR is used to evaluate anything that can fluctuate in value (such as assets and investments). It represents the consistent rate at which an investment would have grown had the investment compounded at the same rate each year.
Why CAGR Is Important
CAGR is a geometric average and provides a more accurate measure of investment than a simple arithmetic mean. It’s typically used to view investments over any period of time, though most often a period of at least 3 to 5 years. It provides the geometric mean return for investments over this time period while accounting for compound growth.
If you’re analyzing investments, this number indicates the value of your investment at the end of that time period (and is particularly useful when comparing or evaluating historical returns of particular investments).
Keep in mind that CAGR assumes a constant growth rate for the time period, which does not reflect the reality of most investment returns. CAGR is simply a way to calculate the internal rate of return, and doesn’t incorporate or consider periodic returns’ variability or standard deviation.
CAGR Formula
The CAGR formula provides a growth rate in the form of a percentage. You might use this formula to project the CAGR needed to achieve your investment goals or measure the return on existing investments.
You can calculate CAGR by using the following formula:

where:
EV = Investment's ending value
BV = Investment's beginning value
n = Number of periods (months, years, etc.)
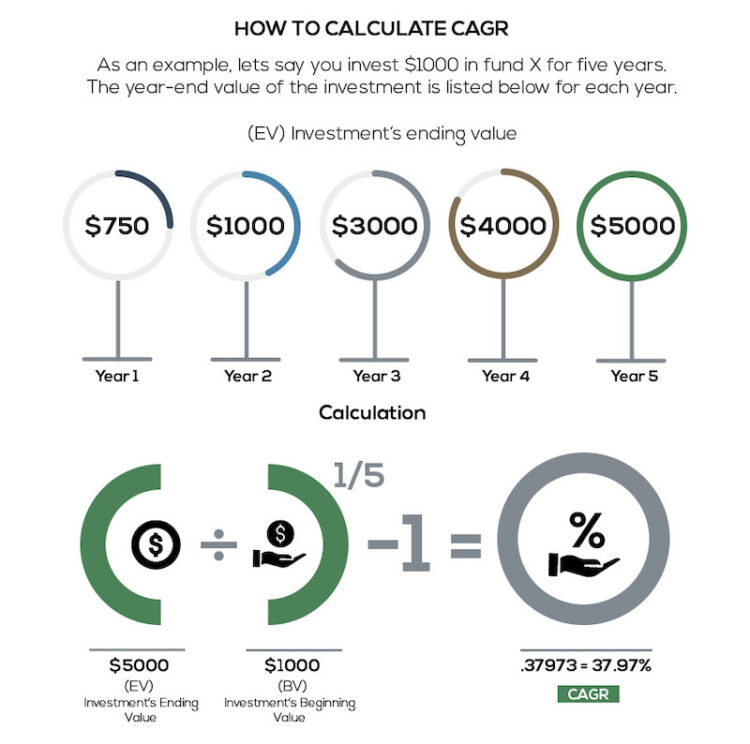
How to Calculate CAGR
As an example, let's say you invest $1,000 in Fund X for five years. The year-end value of the investment is listed below for each year.
Year Ending Value
1 $750
2 $1,000
3 $3,000
4 $4,000
5 $5,000
You can calculate the CAGR of the investment as:
CAGR = (5,000 / 1,000)1/5 - 1 = .37973 = 37.97%
Using the InvestingAnswers’ CAGR calculator, you can easily determine the following:
Calculating CAGR with a Financial Calculator
If you’re using a financial calculator, use the yx button to raise (5,000 / 1,000) to the power of 0.20 (since 1 / 5 = 0.20 ).
Calculating CAGR with Excel
If you need to plug CAGR into an Excel sheet, Excel Easy walks you through that process.
How to Calculate Growth Rate for an Investment
When considering an investment, look at the return from several different lenses by using multiple financial ratios and formulas.
It’s common to use the Average Annual Return (AAR) when looking at mutual funds and other long-term investments. However, CAGR is a better measure of an investment's return over time because it takes investment losses into consideration.
CAGR Example: Return Over Time
For example, consider Year 1 and Year 2 of our hypothetical investment in Fund X. At the end of Year 1, the portfolio value had fallen from $1,000 to $750 for a return of -25% [ (750 - 1,000) / 1,000 ]. By the end of Year 2, the portfolio value had grown by +33% [ (1,000 - 750) / 750 ].
Averaging Year 1 and Year 2 returns over two years gives us an average return of 4% [ (-25 + 33) / 2 ]. But that doesn't accurately reflect what has actually happened. Fund X began with $1,000 and ended with $1,000, which is a return of 0%.
This example shows why CAGR is a better measure of return over time. An average annual return (or arithmetic mean) ignores the effects of compounding and can overestimate growth. CAGR, on the other hand, represents a consistent rate at which the investment would have grown. CAGR will always be equal to or less than the arithmetic mean.
Are CAGR and IRR the Same?
Let’s look at how Internal Rate of Return compares to CAGR. Both formulas measure the returns of investments, but CAGR's formula only includes one initial investment (cash outflow) and one ending amount (cash inflow).
By contrast, IRR can have multiple cash inflows and outflows to measure an investment return.
Because of this versatility, the internal rate of revenue is often used to estimate whether proposed projects can generate a higher return than other investments. IRR is also commonly used by venture capital firms to analyze the growth of company acquisition targets.
CAGR vs. Absolute Return
Absolute returns is a much simpler way to arrive at a total return. It doesn't take into account the rate of return over a period of time, making it easier to compare investments. Absolute value is like measuring how many miles you traveled while CAGR is like measuring how many miles per hour you traveled (aka the rate of speed) .
What Is the Formula for Absolute Return?
The formula for absolute return is:
Absolute Return % = ((ending value - beginning value) / beginning value) x 100)
Say you invested $50 and it evolved into $100. That would make for an absolute return of 100% (or (100 - 50)/50 x 100 = 100%).
While that makes for an eye-popping return that's sure to impress, it may be hard to determine how valuable that is without involving a time element. Is that 100% over five years, or 100% over 20 years?
With the figures in the CAGR definition above, the absolute return would be 567% (or (5000 - 750) / (750) X 100) = 567). Using the Investing Answers CAGR calculator, the total was 37.97%. This makes the CAGR a better measure of growth because it accounts for the 5 years of ups and downs.
Because CAGR measures returns for any time period, you can make equal comparisons of one investment's return to another investment's return.




