What is Negative Amortization?
Negative amortization occurs when the principal balance on a loan (usually a mortgage) increases because the borrower's payments don't cover the total amount of interest that has accrued.
How Does Negative Amortization Work?
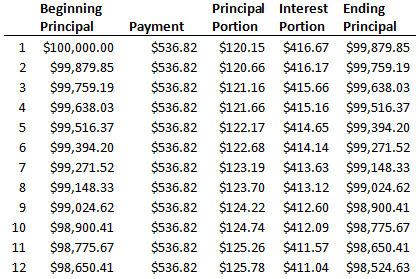
For example, let's assume that John wants to borrow $100,000 from Bank XYZ to buy a house. The interest rate on the 30-year loan is 5%. Normally, this would mean that John would need to make 360 monthly payments of $536.82 in order to pay the loan off in 30 years. Here is how the first 12 months of John's amortization schedule would look under this arrangement (click here to use InvestingAnswers' Amortization Schedule Calculator):
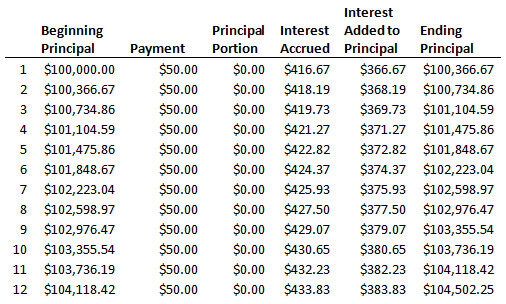
However, Bank XYZ offers John a 'pick your payment' option on his mortgage. Under 'pick your payment,' John can pay as much or as little as he wants for the first year of the mortgage. John decides to pay $50 a month.
What John doesn't realize is that the mortgage accrues at least $410 a month in interest. Because he is only paying $50 each month, the Bank XYZ adds the unpaid interest, $360, to his loan balance every month. The increasing loan balance in turn accrues more interest. Thus, John's loan balance actually goes up each month, and by the end of the first year, he actually owes $104,502 on his $100,000 mortgage. (note that John's $50 payments are applied toward the interest owed first; none of it is applied to the principal balance until the interest portion of the payments is made.)
Why Does Negative Amortization Matter?
Mortgages with 'payment options' often incorporate negative amortization. Rarely do their borrowers understand that paying less than the standard repayment amount will result in a higher loan balance later and more interest later. Nonetheless, they can be very attractive to borrowers who are struggling with payments or expect larger incomes later.
Often, student loans are negatively amortizing loans in the sense that students are not required to make payments while they are still in school but interest continues to accrue and become part of the loan balance. This in turn means that a student who obtains, say, $20,000 of student loans over four years will be surprised to learn on graduation day that his or her beginning loan balance is actually, say, $23,000 -- the extra $3,000 is interest that accrued while the student was still in school.



