What is a Negative Butterfly?
Negative butterfly refers to a change in the yield curve whereby medium-term yields change by a greater magnitude than short-term and long-term yields. It is important to note that the negative butterfly is the opposite of the positive butterfly, where medium-term rates change less than the short-term and long-term rates.
How Does a Negative Butterfly Work?
The yield curve is a graph that plots the yields of similar-quality bonds against their maturities, ranging from shortest to longest. It enables investors at a quick glance to compare the yields offered by short-term, medium-term and long-term bonds. The butterfly is one of three common types of changes in the yield curve (the parallel shift and the twist are the other two). Below are three examples of these patterns.
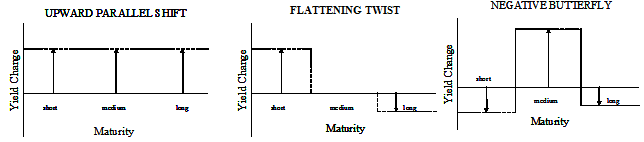
In the real world, changes usually do not affect all sections of the yield curve equally, making the butterfly pattern more common than the parallel shift, for example. Most often, the yield curve steepens and shifts downward or flattens and shifts upward. As a result, the yields of some types of bonds usually change more or less than other types of bonds, and in the case of the negative (or positive) butterfly pattern, this creates or accentuates a hump in the yield curve.
Why Does a Negative Butterfly Matter?
Because the yield curve is generally indicative of future interest rates, which are indicative of an economy's expansion or contraction, yield curves and changes in yield curves can convey a great deal of information. Changes in the shape of the yield curve can also have an impact on portfolio returns by making some bonds more or less valuable relative to other bonds. Thus, if an investor can correctly forecast the direction and type of shift in the yield curve, he or she can buy and sell those securities most affected by those changes.
For example, if the investor believes the yield curve will change in a negative butterfly pattern, then he may believe yields on bonds with short maturities will fall, yields on medium-term bonds will rise, and yields on long-term maturities will fall. Based on this, the investor would shift his portfolio toward the medium-term maturities in order to lock in the higher rates. In a flattening twist, the investor might shift his attention toward short maturities, which have higher yields. A parallel shift in the yield curve requires the least action because the bond yields stay the same relative to each other and thus present little opportunity to take advantage of expected yield changes at different maturities.



