What Is Joint Probability?
Joint probability is a type of measure found by calculating the probability of two events happening together. In other words, it’s the probability of event X happening at the same time as event Y, like an intersection of two events.
Joint Probability for Dependent Events
To measure joint probability, both events need to happen at the same time and must be independent of each other. That means joint probability for dependent events cannot be determined.
Say that you want to determine whether it will rain at the same time that clouds are in the sky. These two events are dependent on each other because when it rains, there will mostly likely be a presence of clouds. Therefore, these events are dependent on each other.
Instead of joint probability, conditional probability should be used for dependent events.
Joint Probability for Independent Events
As mentioned, to determine joint probability, both events need to be independent of each other. For example, the probability of getting “tails” or “heads” on a coin toss are independent events. In other words, the probability of getting a tail on the first toss won’t have an impact of the probability of getting a head when you toss the coin a second time.
How to Calculate Joint Probability
When learning how to calculate joint probability, it’s crucial to understand that the formula requires that the two events be independent of each other. That means the outcome of an event cannot affect the impact of the other event’s outcome. Before you calculate joint probability, ask yourself whether the outcome of one event will influence the outcome of the other.
Since joint probability can be described as “the intersection of two events”, the formula will include the two – and how they can intersect.
In the formula below, you’ll see the symbol “∩” used to represent an intersection. For more visual learners, using a Venn diagram is the best way to illustrate how two events can intersect together.
Joint Probability Formula
The joint probability formula is as follows:
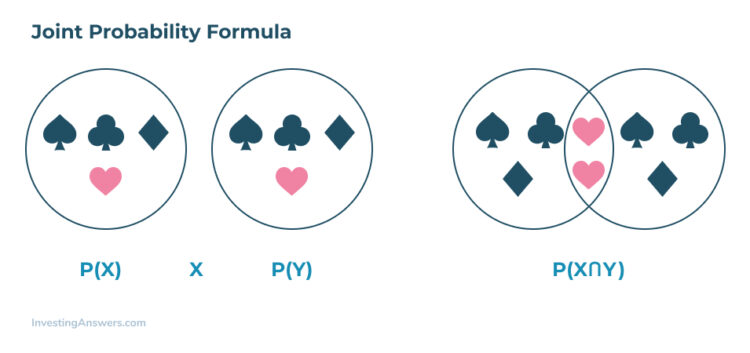
In this formula, X and Y both represent two different events intersecting, and P equals the joining probability of both X and Y.
Other ways to express the joint probability formula also include P( X and Y) and P(XY).
Joint Probability Example #1
Let’s say you want to figure out the joint probability for a coin toss where you can get a tail (Event X) followed by a head (Event Y).
In this instance, the probability of Event X is 50% (or 0.5) and the probability of Event Y is also 50%. Now we can plug in the numbers into the formula:
P(0.5 x 0.5) = 0.25 or 25%
That means, the joint probability of getting a tail and then a head in a coin toss is 25%.
Joint Probability Example #2
You’re rolling a dice and want to figure out the joint probability of rolling the number six twice in a row. The probability of following a six the first time is 1/6, since there are only six options in a six-sided die. This equates to ⅙, or 17% (in decimals that’s 0.1666). It’s the same for rolling a six the second time.
Using this information, we can determine that the joint probability of rolling a six the first and second time will be the following:
P(0.1666 x 0.1666) = 0.02777 or 2.8%
That means you have a 2.8% probability of both events happening.
When to Use Joint Probability
Joint probability is useful when you want to measure two independent events to determine whether they can happen simultaneously.
How is Joint Probability Used in Relation to Investing?
Joint probability is a useful statistic for analysts and statisticians when two or more observable phenomena can occur simultaneously. For example, when a decline in the Dow Jones Industrial Average is accompanied by a substantial loss in the value of the dollar.
You can also compare two separate stocks to see if the value of one goes up (and if the other one will, too).




