What is Macaulay Duration?
The Macaulay duration (named after Frederick Macaulay, an economist who developed the concept in 1938) is a measure of a bond's sensitivity to interest rate changes. Technically, duration is the weighed average number of years the investor must hold a bond until the present value of the bond’s cash flows equals the amount paid for the bond.
How Does Macaulay Duration Work?
There is more than one way to calculate duration (which we'll get to below), but the Macaulay duration (named after Frederick Macaulay, an economist who developed the concept in 1938) is the most common.
The formula for Macaulay duration is:
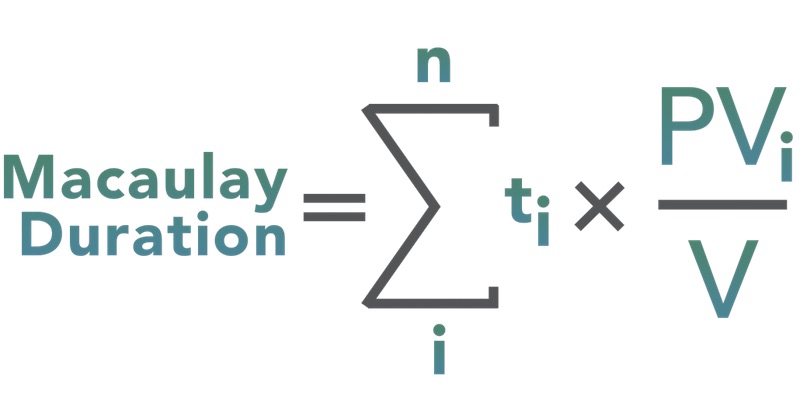
where:
t = period in which the coupon is received
C = periodic (usually semiannual) coupon payment (in $)
y = the periodic yield to maturity or required yield
n = number of periods
M = maturity value (in $)
PV = market price of bond (in $)
The formula is complicated, but what it boils down to is: Duration = Present value of a bond's cash flows, weighted by length of time to receipt and divided by the bond's current market value.
As an example, let's calculate the duration of a three-year, $1,000 Company XYZ bond with a semiannual 10% coupon. By using the present value formula, we can find PV of Cash Flows for each period. So for the first row, we'd figure in ($50) / (1 + .05)^1 = $47.62. For the second row, we'd calculate ($50) / (1 + 0.05)^2 = $45.35. And so on until we make up the following table.
|
Notice in the table above that we first weighted the cash flows by the periods in which the occurred and then calculated the present value of each of these weighted cash flows. There are six periods (three years x 2 semiannual payments per year) and a measure of 5% is used instead of 10% because payments are semiannual.
To calculate the Macaulay duration, we then divide the sum of the present values of these cash flows by the current bond price (which we are assuming is $1,000):
Macaulay duration = $5,329.48 / $1,000 = 5.33
As mentioned earlier, duration can help investors understand how sensitive a bond is to changes in prevailing interest rates.
By multiplying a bond's duration by the change, the investor can estimate the percentage price change for the bond. For example, consider the Company XYZ bonds with a duration of 5.33 years. If market yields increased by 20 basis points(0.20%), the approximate percentage change in the XYZ bond's price would be:
(- Macaulay Duration x Change in Yield) = Approximate Change in Price
-5.33 x 0.002 = -0.01066 or -1.066%
In other words, if the bond had originally sold for $1,000 with a 5% yield it would now be selling for $1,000 x (1 - 0.01066) = $989.34 -- a discounted rate (Note that this is an approximation and is not as precise as a present value of a bond calculator).
Why would the bond be selling for a discount? Because as interest rates go up, other interest-bearing investments become more attractive to investors and thus the bond's value (or price) goes down.
In economics, the simple rule is that yields move in the opposite direction of prices. As yields (i.e. interest rates) go up, bond prices move down. Conversly, as yields go down, bond prices move up.
Expanding on that, there are five factors affect a bond's duration:
- Coupon: The higher a bond's coupon, the more income it produces early on and thus the shorter its duration. The lower the coupon, the longer the duration (and volatility). Zero-coupon bonds, which have only one cash flow, have durations equal to their maturities.
- Maturity: The longer a bond's maturity, the greater its duration (and volatility). Duration changes every time a bond makes a coupon payment. Over time, it shortens as the bond nears maturity
- Yield to Maturity: The higher a bond's yield to maturity, the shorter its duration because the present value of the distant cash flows (which have the heaviest weighting) become overshadowed by the value of the nearer payments.
Sinking Fund: The presence of a sinking fund lowers a bond's duration because the extra cash flows in the early years are greater than those of a bond without a sinking fund.
- Call Provision: Bonds with call provisions also have shorter durations because the principal is repaid earlier than a similar non-callable bond.
Why Does Macaulay Duration Matter?
The greater duration of the bond, the greater its percentage price volatility.
By providing a way to estimate the effect of certain market changes on a bond's price, the investor can choose investments that will better meet his future cash needs. Macaulay duration also helps income investors who want to take on minimal interest rate risk (that is, they believe interest rates might fall) understand why they should consider bonds with high coupon payments and shorter maturities.



