What Is an Interest Rate Swap?
An interest rate swap is a financial contract between two parties (such as companies or investors) that want to exchange interest rates. These could be interest rates they’re paying on loans or rates they’re receiving on investments.
It's important to note that loans and investments aren’t traded or altered: The parties only exchange the interest rates they pay on their loans or receive from their investments.
Which Companies Use Interest Rate Swaps?
Most interest rate swap users are corporations, investors, and banks. Governments also use interest rate swaps.
Why Are Interest Rate Swaps Used?
Corporations, investors, and banks turn to interest rate swaps for a variety of reasons:
To offset the risk of a floating interest rate
To lock into a future fixed rate
To leverage rate differentials between currencies (arbitrage)
To speculate on anticipated rate fluctuations
Where Are Interest Rate Swaps Traded?
Unlike most stocks and bonds that are through exchanges like the New York Stock Exchange, interest rate swaps are traded over the counter (OTC). The trade is made between the counterparties using networks like the one managed by the Financial Industry Regulation Authority. Dealers receive quotes from the networks and make the trades online or by phone.
Are Interest Rate Swaps Cleared?
The Dodd-Frank Wall Street Reform and Consumer Protection Act requires that some interest rate swaps be cleared. The Commodity Futures Trading Commission registers entities called “derivative clearing organizations” for this purpose.
How Does an Interest Rate Swap Work?
Interest rate swaps can get rather complicated, but in their simplest form, they break down into just a few steps:
1. Select a Principal Amount
Once the parties have decided to enter into a swap agreement to exchange interest rates, they have to decide what to base the interest rates on. They settle on a “notional” principal amount which isn’t part of the deal itself, but simply used to indicate the amount on which the interest is being calculated.
2. Define the Rates
The parties must also decide on the type and amount of interest they want to exchange. This interest represents cash flows (i.e. the monies flowing in and out of the swapping companies). When the companies exchange their interest rate payments, they're actually exchanging cash flows.
3. Sign the Interest Rate Swap Contract
The parties sign a financial contract to seal the deal. Commercial or investment banks typically act as an intermediary during this exchange (and are referred to as a “swap bank”). The financial contract used in an interest rate swap is a “derivative” because it derives its value from an underlying asset.
Are Interest Rate Swaps Derivative?
A derivative is a financial contract that receives its value from the exchange of an underlying asset. In the case of an interest rate swap, the interest rate (or the cash flows based on the interest rate) is the asset.
Interest rate swaps and bond futures are both examples of derivatives. Whereas bond futures derive value from the bonds, interest rate swaps get their value from the cash flows being exchanged.
A Simple Interest Rate Swap Example
Company ABC has a $1 million loan with a fixed interest rate, but because the company has predicted a drop in interest rates, it wants to switch to a floating rate.
Company XYZ has a $1 million loan with a floating rate, but it would prefer the predictability of a fixed rate.
These companies can swap their interest rates without affecting their loans – and without involving their loan principals. They do this by entering into a contract to exchange their interest rates. The contract indicates the notional principal, the rates the companies will pay, the due dates for the payments, and the date the swap matures.
Both companies continue making their usual interest payments to their lenders. Company ABC (which swapped its fixed rate for a floating rate) owes Company XYZ the agreed-upon floating rate. Company XYZ (which exchanged its floating rate for a fixed rate) owes Company ABC the agreed-upon fixed rate.
In practice, parties only pay the difference between the fixed and variable interest amounts.
3 Examples of Interest Rate Swaps
Interest rates can be swapped in a few different ways, depending on the needs of the parties to the contract. In each case, the interest rate is based on the notional principal discussed earlier.
1. Fixed-to-Floating Swap Rates
A “vanilla” swap is the most common type of interest rate swap, meaning that the parties exchange a fixed interest rate for a floating interest rate (and vice versa). The fixed rate stays the same for the length of the swap contract. The floating rate is usually based on a benchmark, such as the London Interbank Offered Rate (LIBOR), and it fluctuates with the benchmark.
The floating rate could be set at LIBOR or LIBOR + a markup (known as a credit spread). It’s expressed as, “LIBOR + x%,” where “x” is the credit spread.
So, if LIBOR is 0.25% today – and the spread is 1% – the floating rate is expressed as LIBOR + 1%. The actual rate is 1.25% (0.25% + 1%). If LIBOR were to increase to 0.27% tomorrow, the rate would be 1.27%.
Loan Interest: Fixed to Floating Interest Rate Swap
The following fixed-to-floating examples show how counterparties might swap interest rates on a loan. The second illustrates a swap on investment interest.
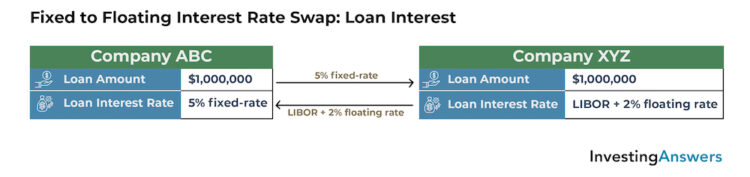
This loan interest rate example assumes:
Company ABC has a $1,000,000 loan with a 5% fixed-rate. The company would prefer a floating rate.
Company XYZ has a $1,000,000 loan with a floating rate of LIBOR, which is currently at 1%, plus a 2% spread. XYZ would prefer a fixed rate.
Under the terms of the swap contract:
Company ABC agrees to pay Company XYZ an annual LIBOR + 2% floating rate on a notional $1,000,000 principal.
Company XYZ agrees to pay Company ABC an annual 5% fixed rate on a notional $1,000,000 principal.
Moving forward, because the loan isn’t affected by the swap, Company ABC continues paying its lender the fixed interest payment of $50,000 (1,000,000 x 5%). Company XYZ pays its lender the floating interest payment of, currently, $30,000 ($1,000,000 x (1% + 2%)). Neither company’s loans have been altered in any way.
Under the terms of the swap agreement, at the end of the year:
Company ABC owes Company XYZ $30,000 (1,000,000 x (1% + 2%)).
Company XYZ owes Company ABC $50,000 (1,000,000 x 5%).
The two transactions partially offset each other, so Company XYZ pays Company ABC the difference of $20,000 ($50,000 - $30,000).
2. Floating to Fixed Swap Rates
A floating to fixed swap represents the position of the company exchanging its floating interest rate for a fixed one. This is the reverse part of the vanilla swap (ie. fixed to floating) explained above.
Investment Interest: Floating to Fixed Interest Rate Swap
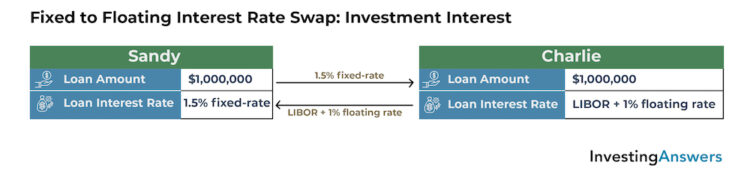
Now, look at the case of an interest rate swap involving two investors. This example assumes:
Sandy owns a $1,000,000 investment that pays her 1.5% every month.
Charlie owns a $1,000,000 investment that pays him LIBOR + 1% every month.
Moving forward, Charlie receives a monthly payment of $12,500 from his investment ($1,000,000 x (0.25% + 1%)). Sandy receives a monthly payment of $15,000 from her investment ($1,000,000 x 1.5%). Neither of their investment principals is affected.
Under the terms of the contract:
Charlie agrees to pay Sandy LIBOR + 1% per month on a $1,000,000 notional principal.
Sandy agrees to pay Charlie 1.5% per month on the notional $1,000,000 principal.
At the end of the month:
Charlie owes Sandy $12,500 ($1,000,000 x LIBOR+1%).
Sandy owes Charlie $15,000 ($1,000,000 x 1.5%).
Since the two transactions partially offset each other, so Sandy pays Charlie the difference of $2,500.
3. Float to Float Swap Rates
Since both parties already pay a floating interest rate, a float-to-float interest rate swap amounts to a basis point exchange. These swap varieties might exchange a floating rate based on one benchmark (such as LIBOR) for a floating rate based on another benchmark (like the US prime rate).
Or, a floating-for-floating swap might exchange for different lengths of time (tenors) within the same benchmark. For example, a one-month LIBOR might be exchanged for a three-month LIBOR.
Float to Float Interest Rate Swap Example
Float-to-float swaps work a little differently because both parties already have floating interest rates. The swap here either exchanges the type of floating rate or the rate’s benchmark. This is considered a basis swap.
For this interest rate swap example, Company ABC has a loan with a floating interest rate indexed to the 1-month LIBOR, but it wants its rate indexed to the 6-month LIBOR. Instead of exchanging a fixed rate for a floating one, it exchanges one type of floating rate for another.
LIBOR isn’t the only interest rate benchmark out there. Company ABC might prefer a rate that is based on a different benchmark and could swap its 1-month LIBOR rate for the US prime rate.
Interest Rate Swap vs. Currency Swap
A currency swap (also called a cross-currency swap) is a contract between parties that want to exchange debt principal and interest from one currency to another. In the process, currency swaps can exchange fixed-to-floating rates or floating-to-floating rates.
A German company may want to swap its EUR-based debt for debt-based in US dollars. The American company wants to swap its USD-based debt for EUR-based debt. The German company would borrow dollars from the American company while the American company would borrow Euros from the German one. They’d repay the loans when the contract matures.
How Interest Rate Swaps Can Be Used for Hedging
Interest rate swaps can be used for hedging, which allows a counterparty to offset the risk of its current interest rate by exchanging it for one it believes will be more favorable in the future.
For example, a company believes that long-term interest rates are likely to rise. It can hedge its exposure to interest rate changes by exchanging its floating rate loan payments for fixed-rate payments. This is a good example of how counterparties might use an interest rate swap for mortgage rates.
Are Interest Rate Swaps Collateralized?
It’s typical for the counterparty with weaker credit to post collateral to mitigate its risk of default.
Risks of Interest Rate Swaps
Two types of risk associated with interest rate swaps are interest rate risk and counterparty risk. Interest rate risk stems from fluctuations in interest rates that can reduce profits. Counterparty risk is the risk that one of the parties will default on the contract. The clearing process (mandated under Dodd-Frank financial protections) reduces – but doesn’t entirely eliminate – counterparty risk.




